ARC004 B問題 : 2点間距離の最大と最小 ( Maximum and Minimum )

問題. 2点間距離の最大と最小 ( Maximum and Minimum )

平面上に $N + 1$ 個の点があり，0 から $N$ まで番号付されている．任意の $i \, (0 \le i < N)$ に対して， $i$ 番目と $i + 1$ 番目の点の間の距離 $d_i$ が与えられる．このとき，0 番目と $N$ 番目の点の間の距離としてとりうる最大値と最小値を答えよ．

制約： $1 \le N \le 500$ ，　 $1 \le d_i \le 30,000$

解法

0 番目の点は原点に固定されているとする．このとき，0 番目の点以外のすべての点の座標は固定されていないので自由に移動させることができるが，2点間の距離は定まっているので下の図（参考元：問題文の図）のようなロボットアームのようなものとなる．
　　　

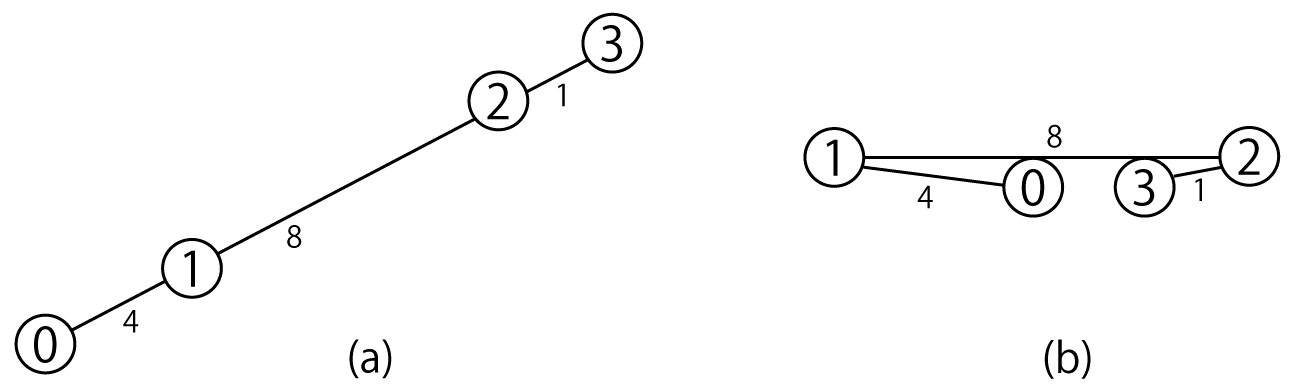
0 番目と $N$ 番目の点の間のとりうる最大距離は，ロボットアームが一直線となっているときで $\sum_{i = 0}^{N -1} d_i$ である．

次に，0 番目と $N$ 番目の点の間のとりうる最小距離について考える．まず，任意の $0 \le i < j < N$ に対して $d_i$ と $d_j$ を交換しても最小距離は変わらないので， $d_0, d_1, \ldots, d_{N - 1}$ は降順にソートされているとする．
1 番目の点が移動することができる領域は原点を中心とした半径 $d_0$ の円周上である（下図の赤色）．次に 2番目の点が移動することができる領域を考えると，下の図のようなドーナッツの領域となる（下図の青色の領域）．
　　　　 f:id:tatanaideyo:20190523213128p:plain:w450

同様に，3番目の点は青色の領域を中心とした半径 $d_2$ の円全体となるので，青色の領域を原点と外側に向かって $d_2$ だけ拡大したドーナッツの領域となる．したがって， $d_0 \le \sum_{i = 1}^{N - 1} d_i$ ならば $N$ 番目の点が移動できる領域は原点を中心とした半径 $\sum_{i = 0}^{N - 1} d_i$ の円板となる．このときは， $N$ 番目の点は原点に移動することができるので最小距離は 0 である．
それ以外のときは，領域は円板とならずにドーナッツの形状をして原点を含まないので最小距離は $d_0 - \sum_{i = 1}^{N - 1} d_i$ である．

計算時間： $O(N)$

ソースコードを表示

#include <bits/stdc++.h>

using namespace std;

using ll = long long;
using ld = long double;

int main() {
    cin.tie(0); ios::sync_with_stdio(false);
    // cout << setprecision(8) << setiosflags(ios::fixed);

    int N;
    cin >> N;

    vector<int> d(N);
    for (auto &d_i : d) cin >> d_i;

    int sum = accumulate(d.begin(), d.end(), 0);
    cout << sum << endl;

    int max_d = *max_element(d.begin(), d.end());
    if (sum < 2 * max_d) cout << 2 * max_d - sum << endl;
    else cout << "0\n";

    return 0;
}

ドーナッツが食べたくなってきた．