ABC131 F問題：Must Be Rectangular!

問題. Must Be Rectangular!

平面上に $n$ 個の点があり， $i$ 番目の点の座標は $(x_i, y_i)$ である． $(a, b), (a, d), (c, b), (c, d)$ 　 $(a \neq c \wedge b \neq d)$ のうち3点が存在するときに残りの1箇所に点を追加するという操作を行う．最大でこの操作を何回行えるかを求めよ．

制約： $1 \le n \le 10^5$ ，　 $1 \le x_i, y_i \le 10^5$

解法

解説を参考にした．

解説通りに二部グラフ $G = (X; Y, E)$ を次のように構成する．
　・ $X = \{1, 2, \ldots, 10^5 \}$ ，　 $Y = \{1, 2, \ldots, 10^5 \}$
　・ $E = \{\{x_i, y_i\} \mid 1 \le i \le n \}$
平面上の点を追加する操作は二部グラフ上で辺を追加する操作に対応する．また， $G$ の異なる連結成分間に辺を加える操作はできない．したがって，各連結成分ごとに加えることができる辺数を求めれば十分である．

$G$ の連結成分数は 1 であると仮定する． $|X| < 2$ または $|Y| < 2$ のときは辺を加えることがきないので，それ以外の場合を考える（細かい場合分けは省略）．

下の証明は間違い（後で直す）
$G$ は完全二部グラフにできることを示すために，任意の頂点 $a, c \in X$ と $b, d \in Y$ を考えて，その誘導部分グラフを完全二部グラフにできることを示す．
まず，最小次数が 2 以上のときは，閉路が存在するので，下の図のように赤い辺 $\{c, d\}$ を加えることができる．
　　　 f:id:tatanaideyo:20190623185036p:plain:w400

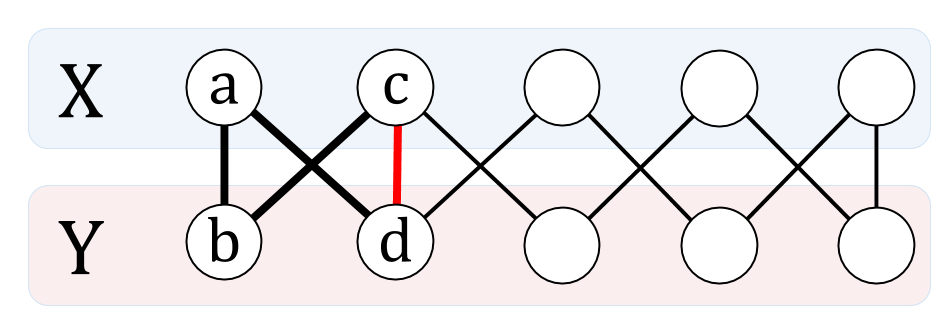
それ以外の場合は次数 1 の頂点が存在する．一般性を失わずに次数 1 の頂点を $a \in X$ とすると，連結性から $\{a, b\} \in E$ かつ $\{b, c\} \in E$ が成り立つ．ここで， $\{c, d\} \in E$ ならば辺 $\{a, d\}$ を加えることができる．それ以外の場合は，連結性から $c$ と $d$ の間に道が存在する．このとき，緑色の辺を右から逐次加えることによって，赤色の辺 $\{c, d\}$ と $\{a, d\}$ を加えることができ， $a, b, c, d$ を完全二部グラフにすることができる．
以上から $G$ は完全二部グラフにすることが可能である．
　　　 f:id:tatanaideyo:20190623185254p:plain:w400

実装では， $|E| \le n$ なので， $G$ を陽に構成して連結成分ごとに DFS で連結成分内の $X$ と $Y$ に属する頂点数を数えた． $i \,(i = 1, 2, \ldots, k)$ 番目の連結成分の $X$ と $Y$ に属する頂点数をそれぞれ $x_i, y_i$ とすると，求める答えは
　　 $\sum_{i = 1}^{k} x_i \times y_i - |E|$
となる．ただし， $x_i < 2$ または $y_i < 2$ となる $i$ 番目の連結成分内の辺数は $x_i \times y_i$ となることに注意が必要である．また， $|E|$ は std::set で $O(n \log n)$ 時間で求めた．

計算時間： $O(n \log n)$

ソースコードを表示

#include <bits/stdc++.h>

using namespace std;

using ll = long long;
using ld = long double;

const int MAX_N = 1e5 + 1;
vector<vector<int>> adj_x(MAX_N), adj_y(MAX_N);
vector<pair<bool, bool>> visited(MAX_N, make_pair(false, false));

void Dfs(const int cur, const bool in_x, ll &num_x, ll &num_y) {
    if (in_x) {
        ++num_x; visited[cur].first = true;
        for (int dst : adj_x[cur])
            if (!visited[dst].second) Dfs(dst, !in_x, num_x, num_y);
    }
    else {
        ++num_y; visited[cur].second = true;
        for (int dst : adj_y[cur])
            if (!visited[dst].first) Dfs(dst, !in_x, num_x, num_y);
    }
}

int main() {
    cin.tie(0); ios::sync_with_stdio(false);
    // cout << setprecision(8) << setiosflags(ios::fixed);

    int n;
    cin >> n;

    set<pair<int, int>> edges;
    for (int i = 0, x, y; i < n; ++i) {
        cin >> x >> y;
        if (edges.count(make_pair(x, y)) == 0) {
            adj_x[x].push_back(y);
            adj_y[y].push_back(x);
            edges.emplace(x, y);
        }
    }

    ll num = 0;
    for (int x = 0; x < MAX_N; ++x) {
        if (visited[x].first) continue;
        ll num_x = 0, num_y = 0;
        Dfs(x, true, num_x, num_y);
        num += (num_x * num_y);
    }

    cout << num - edges.size() << endl;

    return 0;
}

二部グラフと言われればそうなんだけど，そこまでに至る思考過程が難しい．強い人云わく典型らしい（どこらへんかは分からない）．