強 NP 完全性とは？ - 忘れても大丈夫

この記事では、数値を含む判定問題に関係する 強 NP 完全性（強 NP 困難性）、弱 NP 完全性（弱 NP 困難性）、擬多項式時間アルゴリズム、弱多項式時間アルゴリズム、強多項式時間アルゴリズム について、次の論文の内容に沿って紹介する。

[1] M. R. Garey and D. S. Johnson. "Strong" NP-Completeness Results: Motivation, Examples, and Implications. J. ACM 25 (1978) pp. 499–508.
DOI:10.1145/322077.322090

1. はじめに

初めに、この記事で対象となる「数値を含む判定問題」の例として 2 分割問題を紹介する [2]。

2 分割問題（2-partition problem）

入力： $n$ 個の自然数の集合 $A = \{a_1, a_2, \ldots, a_n\} \subseteq \mathbb{N}$
出力： Yes か No
条件： $\sum_{i \in X} a_i = \sum_{i \notin X} a_i$ となる $X \subseteq \{1, 2, \ldots, n\}$ が存在する $\implies$ Yes

　　　　 $\sum_{i \in X} a_i = \sum_{i \notin X} a_i$ となる $X \subseteq \{1, 2, \ldots, n\}$ が存在しない $\implies$ No

例）入力 $A = \{3, 7, 2, 4, 3, 2, 1 \} \; (a_1 = 3, a_2 = 7, \ldots, a_7 = 1)$ ： $X = \{1, 2, 7\}$ で等分割可能なので Yes を出力

＊ここでは数値と言ったら非負整数を表す ~~（整数や有理数も、適当な符号化をすれば自然数として扱える）~~（2025年12月30日修正・追記） 入力として与えられる数値が非負整数ではなく有理数の場合は問題が難しくなる場合があるので注意。

【展開して表示】（補足）入力数値が非負整数と有理数の場合の違い

2 分割問題は NP 完全であることが知られており、また、動的計画法を用いた $O(n T)$ 時間アルゴリズムが存在する（ここで $T = \sum a_i$ ）。数値 $T$ を標準的な 2 進数で符号化するとサイズは $O( \log T)$ となるので、 $O(n T)$ 時間は指数時間となり嬉しくない。ただし、入力の $T$ が $n$ の多項式で制限されるような場合だと $O(n T)$ 時間は多項式時間となり嬉しい。このような 入力に現れる数値が制限された問題 の計算複雑さがどのようになるのかをここでは見ていく。

2. 抽象問題と符号化方式

計算クラス P と NP や、 NP完全性、NP困難性 や 多項式時間多対一帰着（Karp 帰着） は形式言語のレベルで定義された概念である。
上で定義した 2 分割問題などを実際に解くには、まず形式言語のレベルで考えるためにインスタンスをチューリング機械の入力アルファベット上の文字列に変換する必要がある。この変換方式を 符号化方式（encoding scheme）と呼び、符号化する前の問題形式のことを 抽象問題（abstract problem） 、符号化後の問題形式のことを 具象問題（concrete problem） と呼ぶ。今後の説明のために抽象問題 $\Pi$ をインスタンスの集合 $D_\Pi$ と Yes インスタンスの集合 $Y_\Pi \subseteq D_\Pi$ の組 $(D_\Pi, Y_\Pi)$ で表す。

1 つの抽象問題に対する符号化方式は一般にたくさんあるので具象問題もたくさんある。抽象問題の符号化方式を具体的に構成する代わりに、時間計算量などに関係する部分だけに注目して次の 2 つの関数で符号化方式を特徴付ける。

関数 $\rm{Length} \colon D_\Pi \to \mathbb{Z}_{>0}$ ：抽象問題のインスタンスを符号化した後のサイズを表す
関数 $\rm{Max} \colon D_\Pi \to \mathbb{Z}_{>0}$ ：抽象問題のインスタンスに表れる最大の数値の大きさを表す

例えば 2 分割問題の場合だと、各インスタンス $I \in D_\Pi$ に対して、

$\rm{Length}_1 (I) = n +\lceil \log_2 T \rceil$ または $\rm{Length}_2 (I) = n \lceil \log_2 T \rceil$ 、
$\rm{Max}_1 (I) = \max \{a_1, a_2, \ldots, a_n \}$ または $\rm{Max}_2 (I) = \sum a_i (= T)$

などがある。

普通、抽象問題から具象問題への変換では 合理的で（reasonable） 簡潔な（concise） 符号化方式を選ぶと仮定してよい。例えば数値は 2 進数で符号化をする。ただ「合理的」で「簡潔な」という用語は曖昧で定義することが難しいので基本的にはアルゴリズム設計者に委ねられるが、ここでは $\rm{Length}$ と $\rm{Max}$ は次を満たすものだけを考えることにする（読み飛ばしても問題ない）。

【展開して表示】合理的で簡潔な符号化方式の必要条件

　
ここまでの議論を丁寧に解説した本に [3, pp. 872-918] がある。

【展開して表示】（補足）計算モデルと符号化方式の差異

3. 数値問題における三種類の多項式時間

数値問題は私たちがイメージする通りの数値を含む問題で、それを定式化すると次の通りになる。また繰り返しになるが、今後現れる問題は抽象問題を対象としており、具体的な「合理的で簡潔な符号化方式」の代わりに $\rm{Length}$ と $\rm{Max}$ を用いて議論する。

Def. 1. 数値問題（number problem）
$\Pi \text{ が数値問題 } \overset{\mathrm{def}}{\iff} \begin{aligned} &\text{次を満たす多項式} p \text{は存在しない：} \\ &\text{任意のインスタンス } I \in D_\Pi \text{に対して、} \mathrm{Max}(I) \le p(\mathrm{Length}(I)) \end{aligned}$

2 分割問題は数値問題である。例えば $\rm{Length} (I) = n +\lceil \log_2 T \rceil$ 、 $\rm{Max} (I) = T$ とすると、 $\rm{Max}(I)$ は $\rm{Length}(I)$ よりも指数的に大きいのでどの多項式でも抑えることができない。

次に、数値問題で重要となる三種類の多項式時間（擬多項式・弱・強）を定義する。

Def. 2. 多項式時間アルゴリズム

擬多項式時間アルゴリズム（pseudo-polynomial-time algorithm） とは、 $\rm{Length}(I)$ と $\rm{Max}(I)$ の多項式時間で実行できるアルゴリズム
弱多項式時間アルゴリズム（weakly polynomial-time algorithm） とは、 $\rm{Length(I)}$ の多項式時間で実行できるアルゴリズム
強多項式時間アルゴリズム（strongly polynomial-time algorithm）とは、数値の総数の多項式時間で実行できるアルゴリズム

例）入力数値が自然数 $a_1, a_2, \ldots, a_n$

擬多項式時間アルゴリズム：最悪時実行時間 $O(\sum_{i = 1}^n a_i)$ 　（2 進符号化だと指数時間）
弱多項式時間アルゴリズム：最悪時実行時間 $O(\sum_{i = 1}^n \log a_i)$
強多項式時間アルゴリズム：最悪時実行時間 $O(n^2)$

弱多項式と強多項式はいずれも通常の意味での「多項式時間」である。速さの直感は次の通りである。

強多項式時間 > 弱多項式時間 > 擬多項式時間

最初に紹介した 2 分割問題に対する $O(n T)$ 時間の動的計画法は擬多項式時間アルゴリズムである。前に述べた通り、合理的で簡潔な符号化方式だと $O(n T)$ 時間は指数時間となるが、入力の数値が組合せ構造のサイズ（ここでは $n$ ）の多項式に抑えられる問題だとみなすと弱多項式時間アルゴリズムとなる。

強多項式時間は「数値演算を桁数に依らず定数時間で扱う」という理想化に基づく。
線形計画問題の弱多項式時間アルゴリズムは知られているが、有名な未解決問題として、線形計画問題に強多項式時間アルゴリズムが存在するのか？がある（詳しくは藤重悟：「線形計画法の最近の発展　線形計画問題の強多項式解法について」を参照）。

4. 数値問題の NP 完全性

数値問題には様々な多項式時間の定義があることを見てきた。定義から明らかに

強多項式時間アルゴリズムは、弱多項式時間アルゴリズムであり擬多項式時間アルゴリズム
弱多項式時間アルゴリズムは、擬多項式時間アルゴリズム

が成り立つ。そこで計算複雑さの観点から、P $\neq$ NP の仮定の下で、

問題に対する弱多項式時間アルゴリズムが存在しない（ $\therefore$ 強多項式時間アルゴリズムも存在しない）
問題に対する擬多項式時間アルゴリズムが存在しない（ $\therefore$ 弱多項式時間と強多項式時間アルゴリズムも存在しない）

が気になる。1 番目は 弱 NP 完全性（weakly NP-complete） と 弱 NP 困難性（weakly NP-hard） であり、これは普通の意味での NP 完全性（NP 困難性）に対応する。
2 番目は今から定義する強 NP 完全性に対応する概念である。その前に今まで何度か述べてきた「入力の数値が入力サイズの多項式に抑えられる問題」を定義する。

Def. 3. 問題 $\Pi$ と多項式 $p$
　問題 $\Pi_p = \{I \in D_\Pi \mid \rm{Max}(I) \le p(\rm{Length}(I)) \}$

次に主題である強 NP 困難性を定義する。

Def. 4. 強 NP 困難（strongly NP-hard）、強 NP 完全（strongly NP-complete）
$\quad \Pi \text{ が強 NP 困難} \overset{\mathrm{def}}{\iff} \begin{aligned} &\text{ある多項式 } p \text{ が存在して } \Pi_p \text{ が NP 困難} \end{aligned}$

$\quad \Pi \text{ が強 NP 完全} \overset{\mathrm{def}}{\iff} \begin{aligned} & \Pi \text{が強 NP 困難で、かつ、 } \Pi \in NP \end{aligned}$

【展開して表示】Def. NP 困難性と NP 完全性

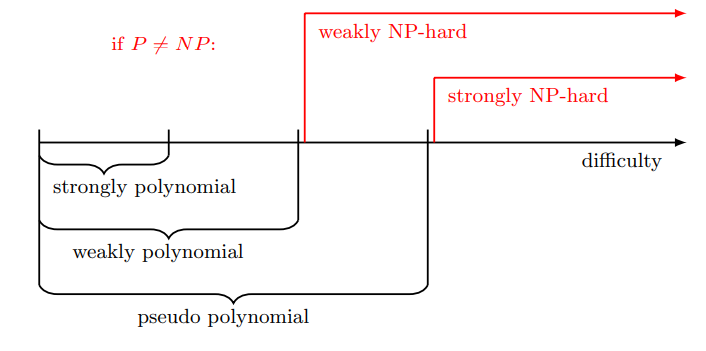
感覚的には、問題が強 NP 困難であるとき、数値が入力サイズの多項式に制限されていても難しいということを意味している。下図は横軸を問題の難しさ（difficulty）としたときの直感的な関係を表している [5, Lecture 2 Scribe Notes p. 3]。
2 分割問題や 0-1 ナップサック問題は弱 NP 完全で擬多項式時間アルゴリズムが存在する問題である。
一方、3 分割問題や箱詰め問題などは強 NP 完全なので、P $\neq$ NP の仮定の下で擬多項式時間アルゴリズムが存在しない問題である。

4.2. 強 NP 困難性の証明方法

問題 $\Pi'$ が強 NP 困難であることを示すひとつの方法を紹介する。 $\Pi'$ の符号化方式を $\rm{Length}' , \rm{Max}'$ とする。

強 NP 困難である数値問題 $\Pi$ を準備（符号化方式を $\rm{Length} , \rm{Max}$ とする）
多項式 $p$ を準備
$\Pi$ から $\Pi'_{p}$ への Karp 帰着 $f \colon D_{\Pi} \to D_{\Pi'_p}$ を構成する

3-1. 任意のインスタンス $I \in D_{\Pi}$ に対して、 $I \in Y_{\Pi} \iff f(I) \in Y_{\Pi'_p}$ を確認
3-2. $f$ の計算時間が $\rm{Length}$ の多項式時間であることを確認
3-3. $f(I) \in D_{\Pi'_p}$ であることを確認

普通の NP 完全性の証明と違うところは 3-2 と 3-3 である。

3-2 では、 $\Pi$ は強 NP 困難なので、ある多項式 $q$ が存在して $\rm{Max}(I) \le q(\rm{Length}(I))$ と仮定してよい。すなわち、Karp 帰着 $f$ の計算時間は $\rm{Length}$ と $\rm{Max}$ の多項式であることを示せばよい。

3-3 は普通の NP 完全性の証明にはない部分である。 $f(I) \in D_{\Pi'_p}$ ということは、 $\rm{Max}'(f(I)) \le p(\rm{Length}'(f(I)))$ を示せばよい。このことは、 $f$ の出力、すなわち問題 $\Pi'$ のインスタンス $f(I) \in D_{\Pi'}$ に含まれる数値がインスタンスのサイズの多項式で抑えられていることを意味する。また、 $f$ は多項式時間なので出力の長さも $\rm{Length}$ と $\rm{Max}$ の多項式に抑えられる。したがって、3-3 は $\rm{Max}'(f(I))$ が $\rm{Length}$ と $\rm{Max}$ の多項式で抑えられることを示せばよい。

4.3. 1 進符号化を用いた帰着との関係

[2] や [5] では様々な問題の弱 NP 完全性や強 NP 完全性を証明しているので参考にするとよい。ただし、次のような入力数値の 1 進符号化（unary encoding） を用いてる点が異なることに注意する必要がある。

$\Pi'$ が強 NP 困難であることを証明するのに、強 NP 困難として知られている問題 $\Pi$ から次を示す。

入力数値が 1 進符号化された 問題 $\Pi$ が、
入力数値が 1 進符号化 された問題 $\Pi'$ に多項式時間多対一帰着可能であること

数値 $T$ を符号化するとき、1 進符号化のサイズは $O(T)$ で、2 進符号化のサイズは $O(\log T)$ であることを思い出すと、「入力数値が1 進符号化された問題」というのは「数値が入力サイズの多項式に抑えられる問題」であり問題 $\Pi_p$ に他ならない。したがって示すことは本質的には同じことである。
[1] の 5 章では 1 進符号化で定義していない理由を述べている。また [5] では Erik Demaine の 1 進符号化へのコメントがあるので両方を下に抜粋する。

【展開して表示】5. Alternative Formulations [1, p. 506] の抜粋

【展開して表示】Erik Demaine の 1 進符号化へのコメント [5, p. 3] の抜粋

5. 観察

[1] の OBSERVATION に対する簡単な証明を与える。

Obs. 1.
$\Pi$ は擬多項式時間可解 $\implies$ 任意の多項式 $p$ に対して、 $\Pi_p$ は多項式時間可解

【展開して表示】Obs. 1. 証明

Obs. 2.
$\Pi$ が強 NP 困難 $\implies$ P $\neq$ NP のとき $\Pi$ は擬多項式時間可解ではない

【展開して表示】Obs. 2. 証明

次の 2 つの観察では、数値を含まない問題では三種類の多項式の区別がないことを述べている。特に Obs. 3 では、数値問題ではない NP 完全（NP 困難）な問題を強 NP 完全（強 NP 困難）とみなして、強 NP 困難性の帰着に用いることができることを表している。

例）強 NP 困難性の証明：「数値問題ではない NP 完全な問題（クリーク問題）」から「数値問題（1 | prec | $\sum U_j$ ）」（詳しい証明）
例）NP 完全性の証明：「強 NP 完全な数値問題（3 分割問題）」から「数値を含まない問題（グラフの最小 $k$ 等分割問題）」（詳しい証明）

Obs. 3.
$\Pi$ は数値問題ではない $\implies$ （ $\Pi$ は多項式時間可解 $\iff$ $\Pi$ は擬多項式時間可解）

【展開して表示】Obs. 3. 証明

Obs. 4.
$\Pi$ は数値問題ではない $\implies$ ［ $\Pi$ は NP 完全（NP 困難） $\iff$ $\Pi$ は強 NP 完全（強 NP 困難）］

【展開して表示】Obs. 4. 証明

最後に擬多項式時間帰着を紹介するが、実際に使われているかは分からないので読み飛ばしてもらっても構わない。

Def. 5. 擬多項式時間帰着（pseudo-polynomial transformation）
判定問題 $\Pi$ から判定問題 $\Pi'$ への擬多項式時間帰着 $f \colon D_\Pi \to D_{\Pi'}$ とは、
　(a) 任意の $I \in D_\Pi$ に対して、 $I \in Y_\Pi \iff f(I) \in Y_{\Pi'}$
　(b) $f$ は $\rm{Max}(I)$ と $\rm{Length}(I)$ の多項式時間で計算可能
　(c) 多項式 $p$ が存在して、任意の $I \in D_\Pi$ に対して、 $p(\rm{Length}'(f(I)) \ge \rm{Length}(I)$
　(d) 多項式 $q$ が存在して、任意の $I \in D_\Pi$ に対して、 $\rm{Max}'(f(I)) \le q(\rm{Max}(I), \rm{Length}(I))$

条件 (c) は帰着後の $\Pi'$ への入力が小さくならないことを言っており、次の OBSERVATION 5 を証明するのに使う。

Obs. 5.
$\Pi$ は強 NP 困難、かつ、 $\Pi$ から $\Pi'$ への擬多項式時間帰着が存在 $\implies$ $\Pi'$ は強 NP 困難

【展開して表示】Obs. 5. 証明

参考文献

[2] 岡本吉央：2019 年度講義離散最適化基礎論『離散最適化における計算困難性』（2025年12月7日アクセス）：特に第8回と第9回を参照
[3] T.コルメン，C.ライザーソン，R.リベスト，C.シュタイン（浅野哲夫・岩野和生・梅尾博司・山下雅史・和田幸一訳）：『アルゴリズムイントロダクション第3版総合版：世界標準MIT教科書』．近代科学社，2013．
[4] Michael Sipser（阿部正幸・植田広樹・藤岡淳・渡辺治訳；太田和夫・田中圭介監訳）：『計算理論の基礎［原著第2版］3. 複雑さの理論』．共立出版，2008.
[5] Erik Demaine: Algorithmic Lower Bounds: Fun With Hardness Proofs. MIT 6.890 Lecture Notes, 2014. URL（2025年12月7日アクセス）
[6] Dominik Wojtczak, On Strong NP-Completeness of Rational Problems. Computer Science - Theory and Applications (CSR 2018), Lecture Notes in Computer Science 10846 (2018) 308--320. DOI:10.1007/978-3-319-90530-3_26. arXiv:1802.09465.（arXiv 版を参照）

強 NP 困難性の 1 進符号化を使う帰着がよく分からなかったので記事に書いたら長くなった。たぶん元論文読んだほうが早い気がする。ただ、 $f(I) \in D_{\Pi'_p}$ の部分は見過ごしやすいので書いてよかった。
5 章の「擬多項式時間アルゴリズムが存在しないなら、FPTAS を持たない（条件ある）」は面白いけど長くなるので省略。

（2025年12月30日追記）数値が非負整数と有理数で問題の難しさが変わることを知らなかったので反省。[6] では有理数版 UNBOUNDED SUBSET SUM 問題を 3-CNF $_{\le 4}$ から帰着している。帰着で構成する有理数が多項式サイズだが、それらの組合せの指数関数的な違いを表現できるのが面白かった。[6] では有理数重み版の問題が強 NP 完全だが FPTAS を持つことも証明している。これは [1] の強 NP 困難ならば FPTAS を持たないに一見矛盾しているように思えるが、[1] では目的関数値を非負整数に制限しているので矛盾していない。