Typical DP Contest R問題 : グラフ

問題. グラフ

$N$ 頂点からなる単純有向グラフ $G$ が与えられる． $G$ の2つの有向道の頂点の和集合のサイズが最も大きいものを求めよ．
制約： $1 \le N \le 300$

解法. 強連結成分分解＋推移閉包＋動的計画法

強連結成分分解を行いDAG上で2つの有向道を探す動的計画法をするところまでは分かったのですが，動的計画法の状態遷移など重要な箇所を埋めることが出来なかったので想定解法を参考にしました．解法は想定解法とまったく同じになってしまったのですが書きます．
　Typical DP Contest ひとこと解法集 - Togetter

この問題で有向道 $P = p_1 p_2 \cdots p_k$ は頂点の重複を許すので，各 $p_i$ に対して同じ強連結成分に属する全ての頂点を $p_i$ から通って $p_i$ に戻ることができます．したがって，考える問題は $G$ を強連結成分分解して各強連結成分を1つの頂点に縮約してDAGにしたときに，各頂点にその強連結成分に属する頂点数を重み付けしたグラフ上で重み和最大の有向道を見つける問題に等しくなります．今後は，変換したグラフを $H = (V, A)$ ，頂点重みを $w \,\colon V \rightarrow \mathbb{Z}_{\ge 0}$ として問題を考えることにして， $H$ の有向道の頂点の重み和をその有向道の重みと呼ぶことにします． $H$ はDAGなので頂点集合 $V = v_1 v_2 \ldots v_n$ はトポロジカルソートされているとします．
問題が1つの有向道を見つける問題ならば， $f(i)$ を頂点 $v_i$ を終点とする重み最大の有向道の値として先頭から動的計画法を行えば求めることができるのですが，2つの有向道を考えると，2つの有向道が通る頂点に対してどう扱えばよいのかで難しくなります．

$f(i, j)$ を互いに素で，終点がそれぞれ $v_i, v_j$ の部分有向道の各重みの和の最大値とします．部分有向道とはある有向道の頂点の部分列です．
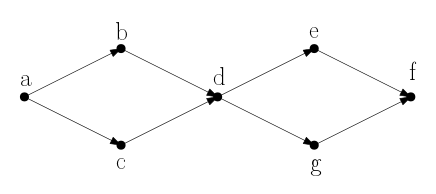
下の例では各頂点の重みを1とします．部分有向道として $abdef$ と $cg$ を考えると2つの重みの和は7となります． $cg$ は例えば有向道 $acdg$ の部分列となっています．
f:id:tatanaideyo:20180628044950p:plain

$f$ に対して動的計画法をするのですが，扱いやすくするために $H$ に重み0の頂点 $v_0$ を加え， $v_0 v_1 \in A$ とします．これは， $f(0, i)$ に対して終点が $v_i$ の部分有向道のみを考えることに対応します．
次に，上の例の部分有向道 $cg$ のようなものを選択しやすくなるように， $H$ の推移閉包を考えます． $H$ の推移閉包とは推移性「 $uv \in A$ かつ $vw \in A$ ならば $uw \in A$ 」を満たすようになるまで $A$ に弧を加えたものです．これは，頂点 $u$ から $w$ へ有向道が存在するならば，弧 $uw \in A$ が存在するように弧を加えたことに等しくなります． $H$ に頂点 $v_0$ を加えて推移閉包したグラフを $H' = (V', A')$ として説明します．
関数 $f$ と $0 \le i < j < k \le n$ に対して，
　 $v_i v_k \in A'$ のとき， $f(j, k) = \max\{f(j, k), f(i, j) + w(v_k)\}$ ,
　 $v_j v_k \in A'$ のとき， $f(i, k) = \max\{f(i, k), f(i, j) + w(v_k)\}$
と更新します．
最大関数の第2引数の $f(i, j) + w(v_k)$ というのは， $v_i v_k \in A'$ のとき，終点 $v_i$ の部分有向道から $v_k$ に飛ぶ部分有向道となり終点を $v_j$ とする部分有向道と互いに素になります．同様に $v_j v_k \in A'$ で考える部分有向道も互いに素になります．ここで， $i \le k \le j$ となる $k$ を考えると互いに素になるとは限らなくなるので注意が必要です．また，任意の $i < j$ に対して帰納法の仮定を満たすように遷移しているので，すべての互いに素な部分有向道を考えていることになります．
以上で求める答えは $\max_{0 \le i < j \le n} f(i, j)$ となります．

計算時間は，強連結成分分解とトポロジカルソートは $O(|V(G)| + |E(G)|)$ ，推移閉包は $O(|V'|^2)$ ，動的計画法は $O(|V'|^3)$ なので全体で $O(|V'|^3)$ になります．
実装では初めに $O(|V|^3)$ 時間で推移閉包をして，トポロジカルソート，動的計画法という流れで行っています．有向グラフに対しての推移閉包はフロイド・ワーシャル法のようにするとできます．

計算時間： $O(N^3)$

ソースコードを表示

#include <bits/stdc++.h>

using namespace std;

int MaximumBlackColor(const int n) {
    // グラフの入力
    vector<vector<bool>> g(n, vector<bool>(n, false));
    for (int i = 0; i < n; ++i)
        for (int j = 0, t; j < n; ++j) { cin >> t; g[i][j] = (t == 1); }


    // 推移閉包
    for (int k = 0; k < n; ++k)
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                if (g[i][k] && g[k][j]) g[i][j] = true;


    // 強連結成分分解
    int N = 1;
    vector<int> size(n + 1), comp(n + 1);
    vector<bool> visited(n, false);
    vector<vector<bool>> h(n + 1, vector<bool>(n + 1, false));

    for (int v = 1; v <= n; ++v) h[0][v] = true;
    for (int v = 0; ; ++N) {
        v = -1;
        // 強連結成分の未訪問の頂点を選択（トポロジカルソートのより先頭）
        for (int u = 0; u < n; ++u) {
            if (visited[u]) continue;

            bool select = true;
            for (int s = 0; s < n; ++s)
                if (u != s && !visited[s] && !(g[s][u] && g[u][s]) && g[s][u]) { select = false; break; }
            if (select) { v = u; break; }
        }

        if (v == -1) break;
        visited[v] = true;
        size[N] = 1;
        comp[v] = N;

        // vと同じ強連結成分内の頂点を探索
        for (int u = 0; u < n; ++u) {
            if (v != u && g[v][u] && g[u][v]) {
                ++size[N];
                visited[u] = true;
                comp[u] = N;
            }
            if (u != v && visited[u] && !(g[v][u] && g[u][v]) && g[u][v]) h[comp[u]][comp[v]] = true;
        }
    }


    // h 上で頂点重み和が最大となる2つの有向道を探す
    vector<vector<int>> dp(N + 1, vector<int>(N + 1));
    for (int i = 0; i <= N; ++i) {
        for (int j = i + 1; j <= N; ++j) {
            dp[i][j] = max(dp[i][j], size[i] + size[j]);
            for (int k = j + 1; k <= N; ++k) {
                if (h[i][k]) dp[j][k] = max(dp[j][k], dp[i][j] + size[k]);
                if (h[j][k]) dp[i][k] = max(dp[i][k], dp[i][j] + size[k]);
            }
        }
    }

    int max_s = 0;
    for (const auto &it : dp)
        max_s = max(max_s, *max_element(it.begin(), it.end()));

    return max_s;
}

int main() {
    cin.tie(0); ios::sync_with_stdio(false);

    int n;
    cin >> n;
    cout << MaximumBlackColor(n) << endl;

    return 0;
}

感想

rng_58さんの解法とソースコードを見て天才か!!とツッコんでしまった（本当に天才なので失礼）．遷移を過不足無く書き出せるの難しい．

問題. グラフ

解法. 強連結成分分解 ＋ 推移閉包 ＋ 動的計画法

感想

解法. 強連結成分分解＋推移閉包＋動的計画法