ABC093 D問題 : Worst Case - 忘れても大丈夫

問題. Worst Case

$10^{10^{10}}$ 人が2回コンテストに参加した．各コンテストでの順位は1位から $10^{10^{10}}$ 位と全員が異なった順位となった．参加者のスコアを2回のコンテストの順位の積としたとき，次の $Q$ 個のクエリを答えよ．
$i$ 番目クエリ $(A_i, B_i)$ はある参加者の1回目と2回目の順位の組である．その参加者よりもスコアが小さい参加者の人数の最大値を答えよ．

制約： $1 \le Q \le 100$ ,　 $1 \le A_i, B_i \le 10^9$

解法. 二分探索

解説を読んでもあまり分からなかったので drkenさんの解説 [2] を参考に解いた．

ある自然数 $x$ に対して， $X = \{1, 2, \ldots, x\} \setminus \{A\}$ ， $Y = \{1, 2, \ldots, x\} \setminus \{B\}$ とすると，問題は次を満たす $E \subseteq X \times Y$ で要素数最大のものを見つける問題に等しい．

　　1. $\forall (a_i, b_i), (a_j, b_j) \in E \, (i \neq j)\, a_i \neq a_j$ かつ $b_i \neq b_j$
　　2. $\forall (a_i, b_i) \in E, \, a_i \times b_i < A \times B$

部集合を $X, Y$ として辺集合を $X \times Y$ とした完全二部グラフ $G = (X; Y, X \times Y)$ を考えると $E$ は $G$ の辺部分集合を選ぶことに対応する．条件 1 は $E$ のどの異なる 2 辺も端点が異なることを表しており，選ぶべき $E$ はマッチングであることを意味している．すなわち， $G$ 上の最大マッチングで条件 2 を満たすものを見つける問題となる．
ここで，条件 2 を満たす $G$ 上の最大マッチング $E^*$ を考える． $E^*$ に飽和されている $X$ と $Y$ の頂点をそれぞれ $a_1 < a_2 < \cdots < a_k$ ， $b_1 < b_2 < \cdots < b_k$ とする．このとき， $(a_{i_1}, b_{i_2}), (a_{j_1}, b_{j_2}) \in E^*$ に対して， $i_1 < j_1$ かつ $i_2 < j_2$ ならば $(a_{i_1}, b_{j_2})$ と $(a_{j_1}, b_{i_2})$ と変更しても条件 1・2 を満たす．また， $a_1 < a_2 < \cdots < a_k$ と $b_1 < b_2 < \cdots < b_k$ を 1 から始まる連番に変更しても条件 1・2 を満たす．ただし，それぞれ $A$ と $B$ の値を含まないものとする．よって，マッチングとして下の図の右のようなマッチングのみを考えることにする．

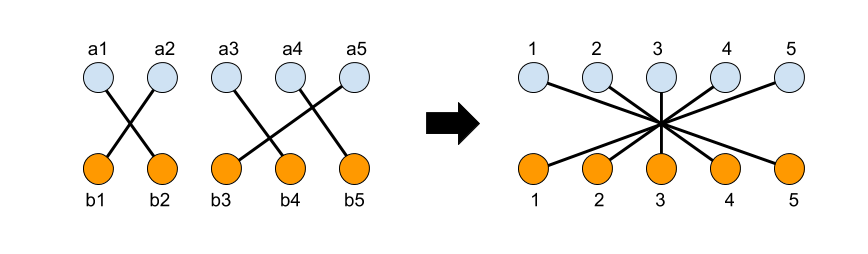
　 f:id:tatanaideyo:20180910160619p:plain:w500

次に自然数 $x$ に対して，完全二部グラフ $G$ 上で右上のようなマッチングで条件 2 を満たすものが存在するかの判定問題を考える．ここで，一般性を失わず $A \le B$ と仮定する．
まず初めに $x < A$ の場合を考える．考えているマッチングでスコアの最大値は，
　 $\max_{1 \le k \le x} k \times (x - k + 1)$
である．これは， $k$ に関しての凹関数であるから偶奇の場合分けをして計算すると，最大値は $\lceil \frac{x}{2} \rceil \times (\lfloor \frac{x}{2} \rfloor + 1)$ となる．すなわち，
　 $\lceil \frac{x}{2} \rceil \times (\lfloor \frac{x}{2} \rfloor + 1) < AB$
ならば右上のようなマッチングが存在して，そのときの参加者数は $x$ 人となる．実は $x < A$ から上の条件は必ず満たすので答えるべき参加者数は $A - 1$ 人以上であることが分かる．
次に， $A \le x < B$ の場合を考える．このマッチングのスコアの最大値は，
　 $\max \left( \max_{1 \le k < A} k \times (x - k + 1), \max_{A + 1 \le k \le x} k \times (x - k + 1) \right)$
となる．これも先程と同様に解くと同じ値となり，最大値は $\lceil \frac{x}{2} \rceil \times (\lfloor \frac{x}{2} \rfloor + 1)$ となり，そのときの参加者数はマッチングの構成方法から $x - 1$ 人となる．
$B \le x$ の場合も同様の結果が得られる．ただし， $2 B \le x$ の場合はマッチングの構成方法からスコアが $\lceil \frac{2 B}{2} \rceil \times (\lfloor \frac{2 B}{2} \rfloor + 1 ) = B \times (B + 1) > A B$ となるので調べる $x$ の上限は $2 B$ より小さいことが分かる．

以上でマッチングのどの辺も交差するようなものを考えることによって，判定問題が凹関数の最大化問題に帰着された（嬉しい）．
$x$ による上の判定問題は単調性を満たすので，条件を満たす $x \in [A, 2B)$ の最大値は二分探索で求めることができ，答えは $x - 1$ となる．各クエリに対して計算時間は $O(\log B)$ となる．

$A$ と $B$ が等しい場合は答えは $2A - 2$ となり，上の計算で求まらないので注意が必要．

計算時間： $O(Q \log( \max\{A + B\} ))$

ソースコードを表示

#include <bits/stdc++.h>

using namespace std;

using ll = long long;

ll Solve(ll a, ll b) {
    if (a == b) return 2 * a - 2;

    if (b < a) swap(a, b);

    ll lb = a, ub = 2 * b, ab = a * b;
    while (1 < ub - lb) {
        ll mid = 0.5 * (lb + ub);
        ll max_p = (mid + 1) / 2 * (mid / 2 + 1);
        if (max_p < ab) lb = mid;
        else ub = mid;
    }

    return lb - 1;
}

int main() {
    cin.tie(0); ios::sync_with_stdio(false);

    int q;
    cin >> q;
    while (q--) {
        ll a, b;
        cin >> a >> b;
        cout << Solve(a, b) << '\n';
    }

    return 0;
}